Functors, Applicatives, And Monads In Pictures (In TypeScript)

Here’s a simple value:

And we know how to apply a function to this value:

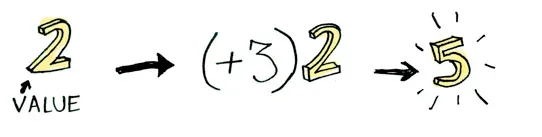
console.log((x => x + 3)(2))
// 5

Simple enough. Lets extend this by saying that any value can be in a context. For now you can think of a context as a box that you can put a value in:

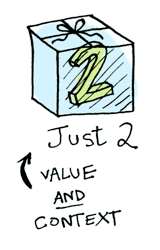
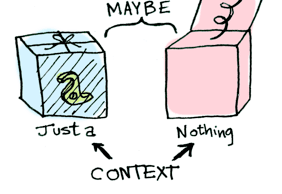
Now when you apply a function to this value, you’ll get different results depending on the context. This is the idea that Functors, Applicatives, Monads, Arrows etc are all based on. The Maybe data type defines two related contexts:

In Haskell

data Maybe a = Nothing | Just a

In TypeScript

type Nothing = null;
type Just<A> = { just: A };

type Maybe<A> = Nothing | Just<A>;

In a second we’ll see how function application is different when something is a Just<A> versus a Nothing. First let’s talk about Functors!

Functors

When a value is wrapped in a context, you can’t apply a normal function to it:

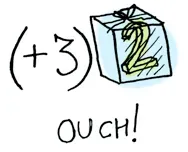
trying to apply a function to a wrapped value

This is where fmap comes in. fmap is from the street, fmap is hip to contexts. fmap knows how to apply functions to values that are wrapped in a context. For example, suppose you want to apply (+3) to Just 2. Use fmap:

In Haskell

> fmap (+3) (Just 2)
Just 5

In TypeScript

// we need do define fmap for our Maybe type in TypeScript
function fmapMaybe<A, B>(f: (a: A) => B, m: Maybe<A>): Maybe<B> {
  if (!m) {
    return undefined;
  }
  return { just: f(m.just) };
}

console.log(fmapMaybe((x) => x + 3, { just: 2 }))
// { just: 5 }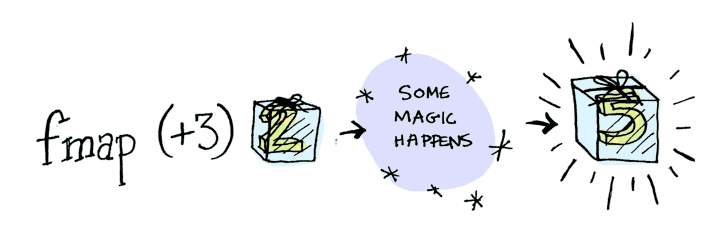

Bam! fmap shows us how it’s done! But how does fmap know how to apply the function? (In this TypeScript translation, we already had to create our own fmap function for Maybe)

Just what is a Functor, really?

Functor is a typeclass. Here’s the definition:

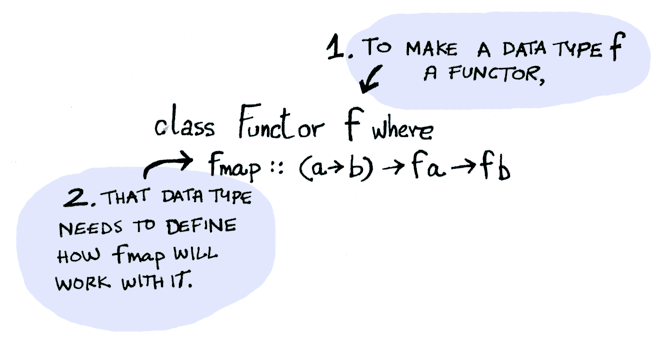
A Functor is any data type that defines how fmap applies to it. In TypeScript, we don’t have typeclasses, so we have to think of a functor as any data type that we have a fmap-like function defined for.

Here’s how fmap works illustrated in Haskell:

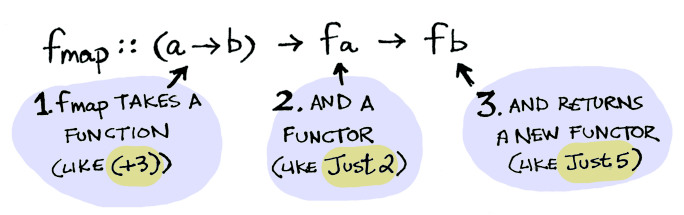
and here’s the same idea in TypeScript

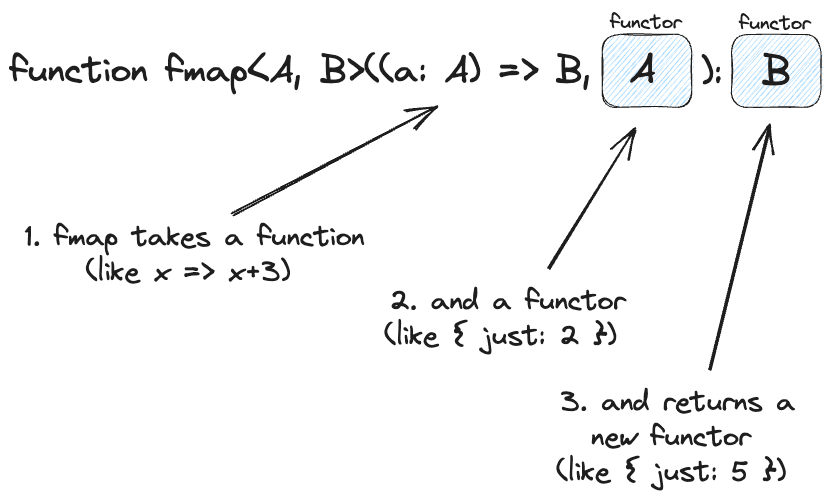
So we can do this in Haskell:

> fmap (+3) (Just 2)
Just 5

Or this in TypeScript:

console.log(fmap(x => x + 3, { just: 2 }));
// { just: 5 }

And fmap magically applies this function, because Maybe is a Functor. It specifies how fmap applies to Justs and Nothings:

instance Functor Maybe where
    fmap func (Just val) = Just (func val)
    fmap func Nothing = Nothing

In TypeScript things are not quite so magical. We can’t just use fmap for any type of Functor. (Unless we wanted to make one big fmap function and then use type-narrowing for whatever type of Functor we throw at it… but let’s not do that.) If we want a data type to be a Functor, we need to define a fmap-like function for it. Here’s our function to make Maybe into a Functor:

function fmapMaybe<A, B>(f: (a: A) => B, m: Maybe<A>): Maybe<B> {
  // if we have a Nothing, return Nothing
  if (!m) {
    return m;
  }
  // if we have a Just, return a Just with the function
  // applied to the contents 
  return { just: f(m.just) };
}

Here’s what is happening behind the scenes when we write fmap (+3) (Just 2) in Haskell, or fmapMaybe(x => x + 3, { just: 2 }) in Typescript:

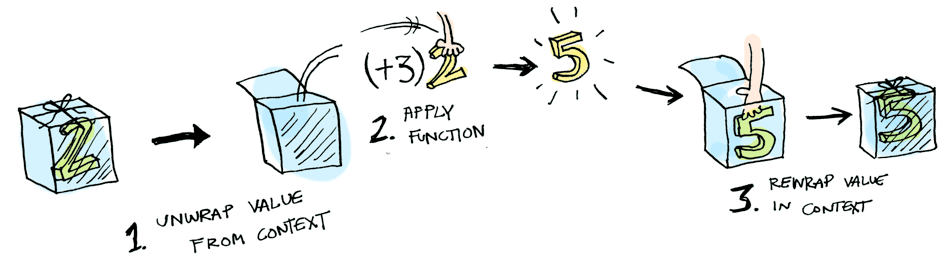
So then you’re like, alright fmapMaybe, please apply x => x + 3 to a Nothing?

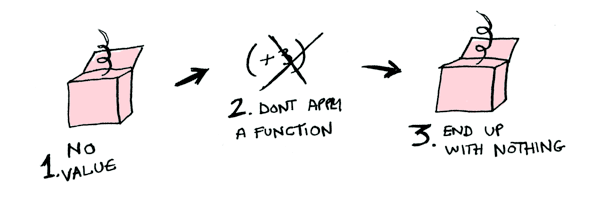
In Haskell

> fmap (+3) Nothing
Nothing

In TypeScript

console.log(fmapMaybe(x => x + 3, undefined));
// undefined

Like Morpheus in the Matrix, fmap knows just what to do; you start with Nothing, and you end up with Nothing! fmap is zen. Now it makes sense why the Maybe data type exists. For example, here’s how you work with a database record in a language without Maybe:

post = Post.find_by_id(1)
if post
  return post.title
else
  return nil
end

But in Haskell:

fmap (getPostTitle) (findPost 1)

Or in TypeScript with our Maybe data type:

fmapMaybe(getPostTitle, findPost(1));

If findPost returns a post, we will get the title with getPostTitle. If it returns Nothing, we will return Nothing! Pretty neat, huh? <$> is the infix version of fmap in Haskell, so you will often see this instead:

getPostTitle <$> (findPost 1)

In TypeScript, we can’t define infix operators / functions, so no fancy <$> for TypeScript … 😔

Here’s another example: what happens when you apply a function to a list?

Lists are functors too! Here’s the definition in Haskell:

instance Functor [] where
    fmap = map

In TypeScript we use Array instead of list, and Array is a functor because it has a method called Array.map() which works as fmap for arrays.

console.log([2,4,6].map((x) => x + 3));
// [5,7,9]

Okay, okay, one last example: what happens when you apply a function to another function in Haskell?

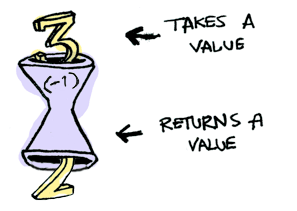
fmap (+3) (+1)

Here’s a function:

Here’s a function applied to another function:

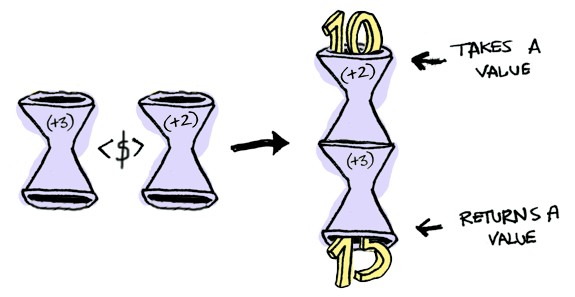
The result is just another function!

> import Control.Applicative
> let foo = fmap (+3) (+2)
> foo 10
15

So, in Haskell functions are Functors too!

instance Functor ((->) r) where
    fmap f g = f . g

When you use fmap on a function, you’re just doing function composition!

In TypeScript we have to do a bit more work to make functions composable and fmap-able:

function compose<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
  return function(x: A): C {
    return g(f(x));
  }
}

function fmapFunction<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
  return compose(f, g);
}

Applicatives

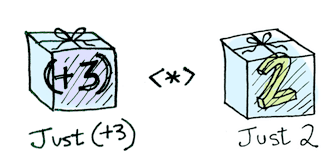
Applicatives take it to the next level. With an applicative, our values are wrapped in a context, just like Functors:

But our functions are wrapped in a context too!

Yeah. Let that sink in. Applicatives don’t kid around. In Haskell, Control.Applicative defines <*>, which knows how to apply a function wrapped in a context to a value wrapped in a context:

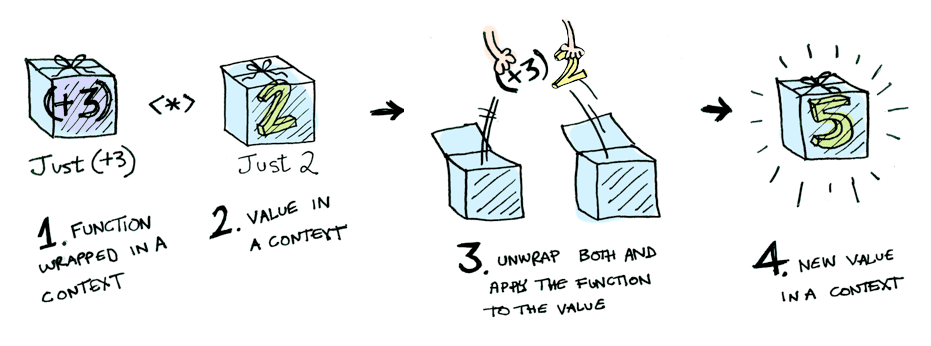
i.e: (in Haskell)

Just (+3) <*> Just 2 == Just 5

In TypeScript we will have to define something like the <*> operator (often called apply) if we want a data type to be an Applicative.

Let’s define an applicative apply function for our Maybe data type:

function applyMaybe<A, B>(f: Maybe<(a: A) => B>, m: Maybe<A>): Maybe<B> {
  // if the function Maybe is Nothing, return Nothing
  if (f === undefined) {
    return undefined;
  }
  // if the data Maybe is Nothing, return Nothing
  if (m === undefined) {
    return undefined;
  }
  // else apply the function in the Maybe
  // to the data in the Maybe
  return { just: f.just(m.just) };
}

console.log(applyMaybe({ just: x => x + 3 }, { just: 2 }));
// { just: 5 }

Using <*> in Haskell can lead to some interesting situations. For example:

> [(*2), (+3)] <*> [1, 2, 3]
[2, 4, 6, 4, 5, 6]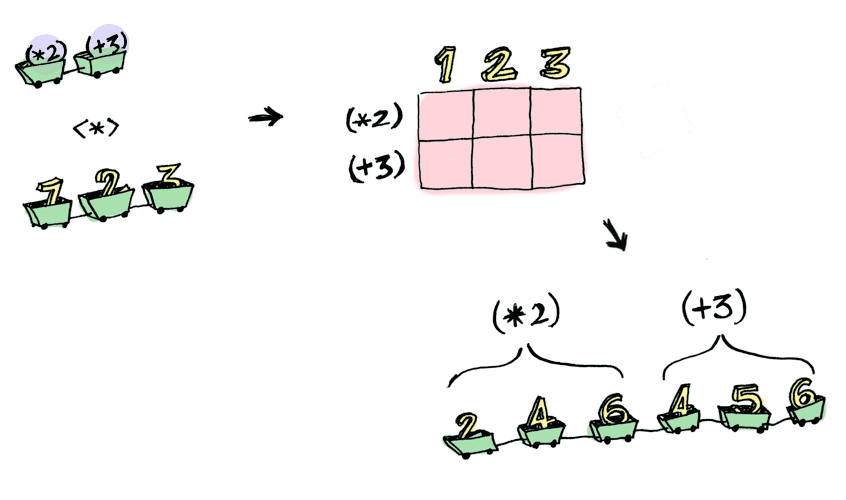

Here we applied a list of functions to a list of values. The <*> function then takes each of the functions in the list and applies them to all the values in the other list.

In TypeScript, we would have to define an apply function for the Array data type to make it an Applicative:

function applyArray<A, B>(fa: ((a: A) => B)[], arr: A[]): B[] {
  // apply each function in the array
  // to each element in the other array
  return fa.flatMap(f => arr.map(f));
}

console.log(applyArray(
  [
    x => x * 2,
    x => x + 3,
  ],
  [1, 2, 3],
));
// [2,4,6,4,5,6]

Here’s something you can do with Applicatives that you can’t do with Functors. How do you apply a function that takes two arguments to two wrapped values?

First let’s look at in in Haskell. This may seem very strange, but you can scroll down to our TypeScript ~~imitation~~ translation below…

> (+) <$> (Just 5)
Just (+5)
> Just (+5) <$> (Just 4)
ERROR ??? WHAT DOES THIS EVEN MEAN WHY IS THE FUNCTION WRAPPED IN A JUST

Applicatives:

> (+) <$> (Just 5)
Just (+5)
> Just (+5) <*> (Just 3)
Just 8

Applicative pushes Functor aside. “Big boys can use functions with any number of arguments,” it says. “Armed <$> and <*>, I can take any function that expects any number of unwrapped values. Then I pass it all wrapped values, and I get a wrapped value out! AHAHAHAHAH!”

> (*) <$> Just 5 <*> Just 3
Just 15

And hey! There’s a function called liftA2 that does the same thing:

> liftA2 (*) (Just 5) (Just 3)
Just 15

For those not familiar with Haskell, these last examples might seem especially confusing. This works in Haskell because of curried functions, and to imitate this magic in TypeScript, we will have to define our own curried versions of + and *

typescript curry imitation of haskell meme

const add = (a: number) => (b: number) => a + b;
const multiply = (a: number) => (b: number) => a * b;

Now that we have curried functions we can do something similar in TypeScript:

fmapMaybe(add, { just: 5 });
// { just: (b) => a + b }

Do you see what happened there? We applied the first argument of the add function to the 5 inside the Maybe, and now we have the other half of the add function in a Maybe. It’s like a function that’s waiting for us to give a b to, and it will give us 5 + b back.

We can’t just throw another fmap around it to finish the job:

const x = fmapMaybe(add, { just: 5 });
fmapMaybe(
  x, // TypeError: x is not a function
  { just: 3 },
)

This doesn’t work because we’re not giving fmap a function like it asks for. We’re giving it a function wrapped in a Maybe. How can we apply a function wrapped in a Maybe ?? That’s exactly what applyMaybe is for!

const x = fmapMaybe(add, { just: 5 });
// x = { just: (b) => a + b }
applyMaybe(x, { just: 3 });
// { just: 8 }

Here’s another example of the same thing with our curried multiply function:

applyMaybe(
  fmapMaybe(multiply, { just: 5 }),
  { just: 3 }
)
// { just: 15 }

Haskell has liftA2 to do the same thing, so let’s define that for our Maybe type in TypeScript.

function liftA2Maybe<A, B, C>(
  f: (a: A) => (b: B) => C,
  a: Maybe<A>,
  b: Maybe<B>
): Maybe<C> {
  return applyMaybe(fmapMaybe(f, a), b);
}

liftA2Maybe(add, { just: 2 }, { just: 3 });
// 5
liftA2Maybe(multiply, { just: 10 }, { just: 3 });
// 30

In Haskell, the Applicative typeclass also defines a function pure which takes a value and wraps in it the data type, so for completeness, we can also define a function pureMaybe to make our Maybe data type into a real Applicative.

function pureMaybe<A>(a: A): Maybe<A> {
  return { just: A };
}

Monads

How to learn about Monads:

Get a PhD in computer science.
Throw it away because you don’t need it for this section!

Monads add a new twist.

Functors apply a function to a wrapped value:

Applicatives apply a wrapped function to a wrapped value:

Monads apply a function that returns a wrapped value to a wrapped value. Monads in Haskell have a function >>= (pronounced “bind”) to do this.

Let’s see an example. Good ol’ Maybe is a monad:

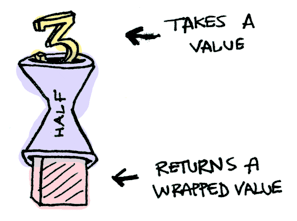
Suppose half is a function that only works on even numbers:

In Haskell:

half x = if even x
           then Just (x `div` 2)
           else Nothing

In TypeScript:

function isEven(n: number): boolean {
  return n % 2 === 0;
}

function half(n: number): Maybe<number> {
  if (isEven) {
    return { just: n / 2 };
  } else {
    return undefined;
  }
}

What if we feed it a wrapped value?

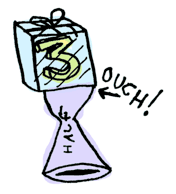
In Haskell we need to use >>= (bind) to shove our wrapped value into the function. Here’s a photo of >>=:

Here’s how it works in Haskell:

> Just 3 >>= half
Nothing
> Just 4 >>= half
Just 2
> Nothing >>= half
Nothing

What’s happening inside? Monad is another typeclass. Here’s a partial definition:

class Monad m where
    (>>=) :: m a -> (a -> m b) -> m b

Where >>= is:

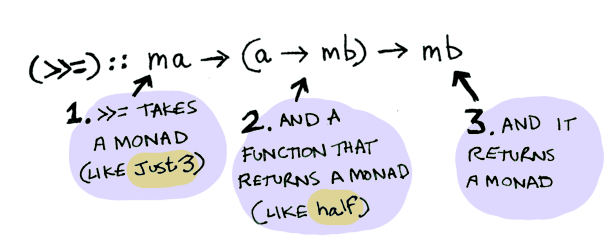
So Maybe is a Monad:

instance Monad Maybe where
    Nothing >>= func = Nothing
    Just val >>= func  = func val

Let’s define a bindMaybe function for our Maybe type in TypeScript, so that Maybe can be a Monad in TypeScript too!

function bindMaybe<A, B>(f: (a: A) => Maybe<B>, a: Maybe<A>): Maybe<B> {
  // if there is no value in Maybe, return Nothing
  if (!a) {
    return undefined;
  }
  // 🪠 unwrap the value in Maybe
  const val = a.just;
  // apply the function to the value
  return f(val);
}

Here it is in action with a Just 3!

And if you pass in a Nothing it’s even simpler:

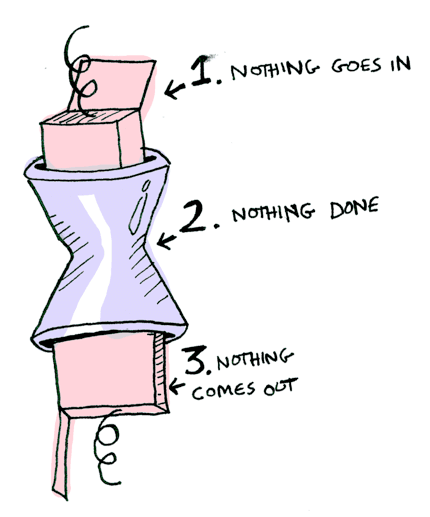
You can also chain these calls:

In Haskell:

> Just 20 >>= half >>= half >>= half
Nothing

In TypeScript:

bindMaybe(
  half,
  bindMaybe(half, 
    bindMaybe(half, { just: 20 })
  )
);
// undefined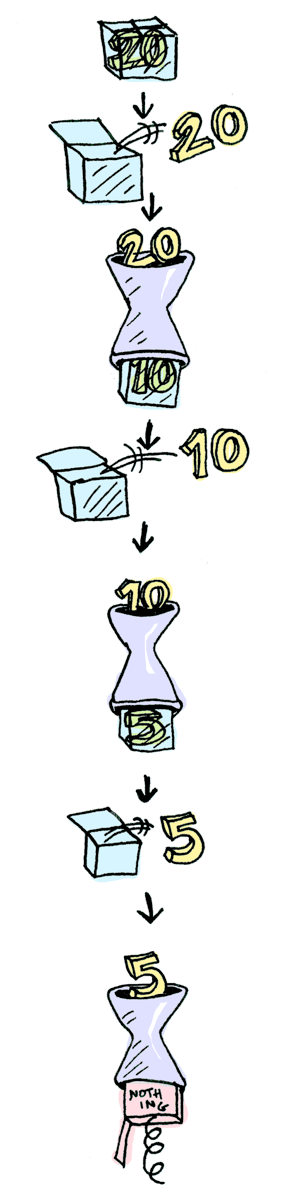

Cool stuff! So now we know that Maybe is a Functor, an Applicative, and a Monad.

Just for completeness, we should also mention that Monads are defined with another function called return which takes a plain value and returns it wrapped in the data type of our Monad. This is the same thing as pure in the Applicative.

function returnMaybe<A>(a: A): Maybe<A> {
  return { just: A };
}

Now let’s mosey on over to another example in Haskell: the IO monad:

Specifically three functions. getLine takes no arguments and gets user input:

getLine :: IO String

readFile takes a string (a filename) and returns that file’s contents:

readFile :: FilePath -> IO String

putStrLn takes a string and prints it:

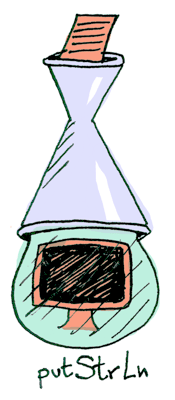
All three functions take a regular value (or no value) and return a wrapped value. We can chain all of these using >>= (bind)!

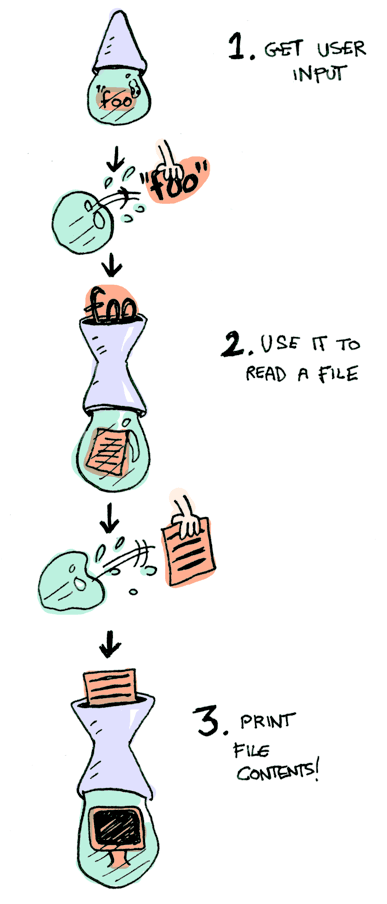
getLine >>= readFile >>= putStrLn

Aw yeah! Front row seats to the monad show!

So what’s the gooey green wrapping in all of this? You can think of it as all the slimy side effects and execution going on in our machine. The values that we want are passed along in this slimy green wrapper, and if at one point in the execution something fails, it just bubbles up an error.

Haskell also provides us with some syntactical sugar for monads, called do notation:

foo = do
    filename <- getLine
    contents <- readFile filename
    putStrLn contents

As Joel Kaasinen and John Lång pointed out in this excellent Haskell MOOC, JavaScript / TypeScript does something very similar with Promises, although there is much disagreement about whether they are really monads.

Promise.then works a lot like >>= (bind).

import prompt from "prompt-async";
import fs from "fs";

prompt.get(["filename"]).then(filename => {
  fs.promises.readFile(filename).then(contents => {
    console.log(contents);
  })
});

Just like the bind or >>= function, the Promise.then() method take a function that takes a plain value and returns another value wrapped in a Promise. (You can also return a plain value though.)

And the async notation used for promises also looks and works just like the do notation for monads in Haskell!

async function printFile() {
  const filename = await prompt.get(["filename"]);
  const contents = await fs.promises.readFile(filename);
  console.log(contents);
}

Conclusion

In Haskell:

A functor is a data type that implements the Functor typeclass.
An applicative is a data type that implements the Applicative typeclass.
A monad is a data type that implements the Monad typeclass.
A Maybe implements all three, so it is a functor, an applicative, and a monad.

Or in TypeScript for our purposes…

A function is a data type that has an fmap function defined for it.
An applicative is a data type that have apply and pure functions defined for it.
A monad is a data type that has bind and return functions defined for it.
Our Maybe data type implements all three, so it is a functor, an applicative, and a monad.

What is the difference between the three?

functors: you apply a function to a wrapped value using fmap or <$>
applicatives: you apply a wrapped function to a wrapped value using <*> or liftA
monads: you apply a function that returns a wrapped value, to a wrapped value using >>= or lift

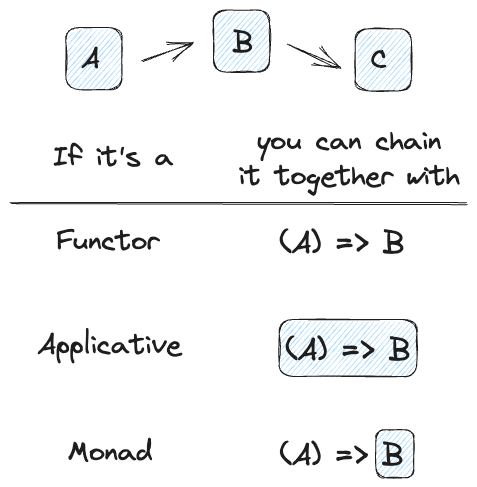
Here’s a visual recap of the general concepts in TypeScript style:

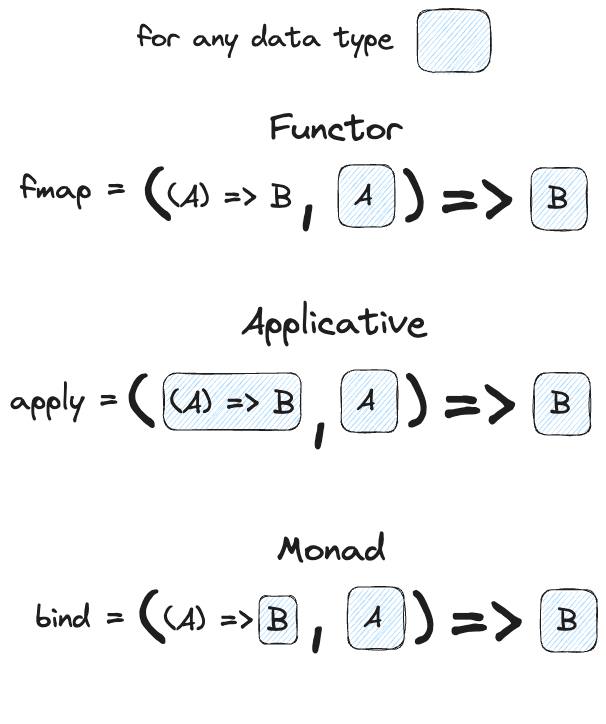
summary of functor (fmap), applicative (apply), and monad (bind) in basic TypeScript types

Notice how the only thing that changes in all three is the function passed in on the left? So we can see that these are all different ways of getting from a wrapped A to a wrapped B.

summary of functor, applicative, and monad in basic TypeScript types

So, dear friend (I think we are friends by this point), I think we both agree that monads are easy and a SMART IDEA(tm). Now that you’ve wet your whistle on this guide, why not pull a Mel Gibson and grab the whole bottle. Check out LYAH’s section on Monads. There’s a lot of things I’ve glossed over because Miran does a great job going in-depth with this stuff.

Here’s a sandbox with our Maybe (functor/applicative/monad) defined below:

This has been a translation and adaptation of of Functors, Applicatives, And Monads In Pictures by Adit into TypeScript.